“Resampling Conserves Redundancy (Approximately)” by johnswentworth, David Lorell

Audio note: this article contains 182 uses of latex notation, so the narration may be difficult to follow. There's a link to the original text in the episode description.

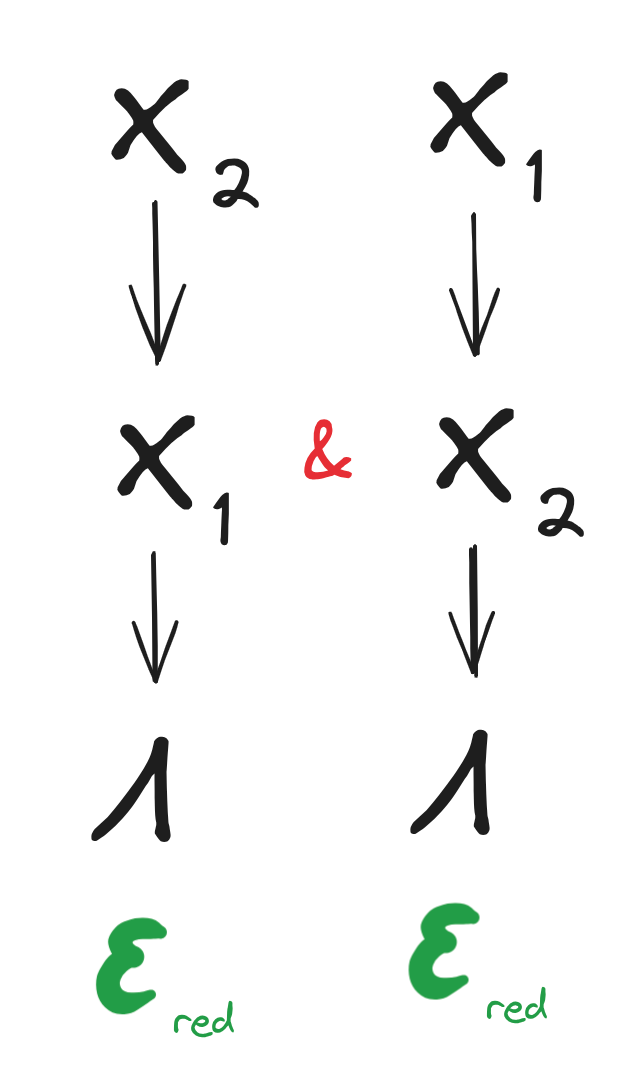
Suppose random variables <span>_X_1_</span> and <span>_X_2_</span> contain approximately the same information about a third random variable <span>_Lambda_</span>, i.e. both of the following diagrams are satisfied to within approximation <span>_epsilon_</span>:

We call <span>_Lambda_</span> a "redund" over <span>_X_1, X_2_</span>, since conceptually, any information <span>_Lambda_</span> contains about <span>_X_</span> must be redundantly represented in both <span>_X_1_</span> and <span>_X_2_</span> (to within approximation).

Here's an intuitive claim which is surprisingly tricky to prove: suppose we construct a new variable Lambda' by sampling from <span>_P[Lambda|X_2]_</span>, so the new joint distribution is

<span>_P[X_1 = x_1, X_2 = x_2, Lambda' = lambda'] = P[X_1 = x_1, X_2 = x_2]P[Lambda = lambda' | X_2 = x_2]_</span>

By construction, this "resampled" variable satisfies one of the [...]

---

Outline:

(02:07) Notation

(02:27) Proof

(03:36) Step 1: Scaling Down The Errors

(05:37) Step 2: Second Order Approximation

(05:42) Validity

(06:40) Expansion

(07:36) Step 3: Good Ol Euclidean Geometry

(07:59) Jensen

(09:12) Euclidean Distances

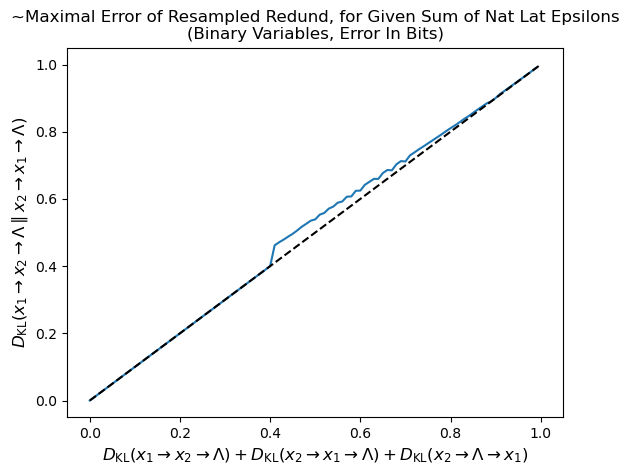
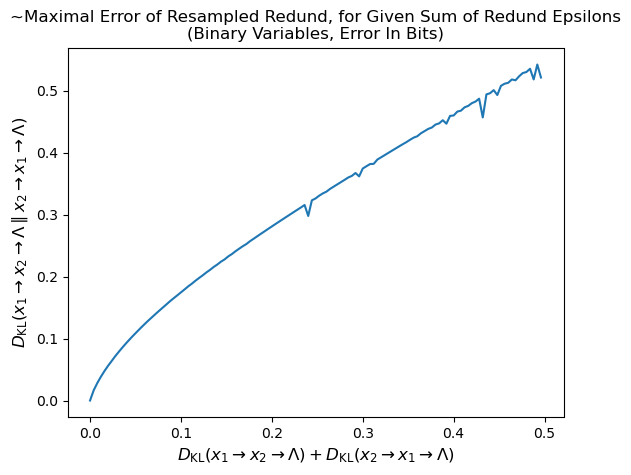
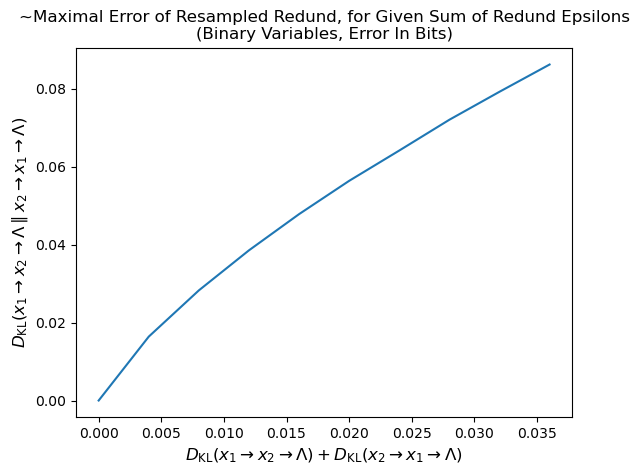
(10:11) Empirical Results and Room for Improvement

The original text contained 2 footnotes which were omitted from this narration.

---

First published:

August 21st, 2025

Source:

https://www.lesswrong.com/posts/cpxxfagD92ivLZCp4/resampling-conserves-redundancy-approximately

---

Narrated by TYPE III AUDIO.

---

Images from the article:

---

---

---

Apple Podcasts and Spotify do not show images in the episode description. Try Pocket Casts, or another podcast app.