“Natural Latents: Latent Variables Stable Across Ontologies” by johnswentworth, David Lorell

Audio note: this article contains 369 uses of latex notation, so the narration may be difficult to follow. There's a link to the original text in the episode description.

This post is an overhaul of (and large improvement to) a paper we wrote about a year ago. The pdf version will hopefully be up on arxiv shortly, and we will link that from here once it's available. As of posting, this is probably the best first-stop mathematical intro to natural latents.

Abstract

Suppose two Bayesian agents each learn a generative model of the same environment. We will assume the two have converged on the predictive distribution (i.e. distribution over some observables in the environment), but may have different generative models containing different latent variables. Under [...]

---

Outline:

(00:52) Abstract

(01:42) Background

(04:12) The Math

(04:15) Setup & Objective

(07:05) Notation

(09:45) Foundational Concepts: Mediation, Redundancy & Naturality

(12:59) Core Theorems

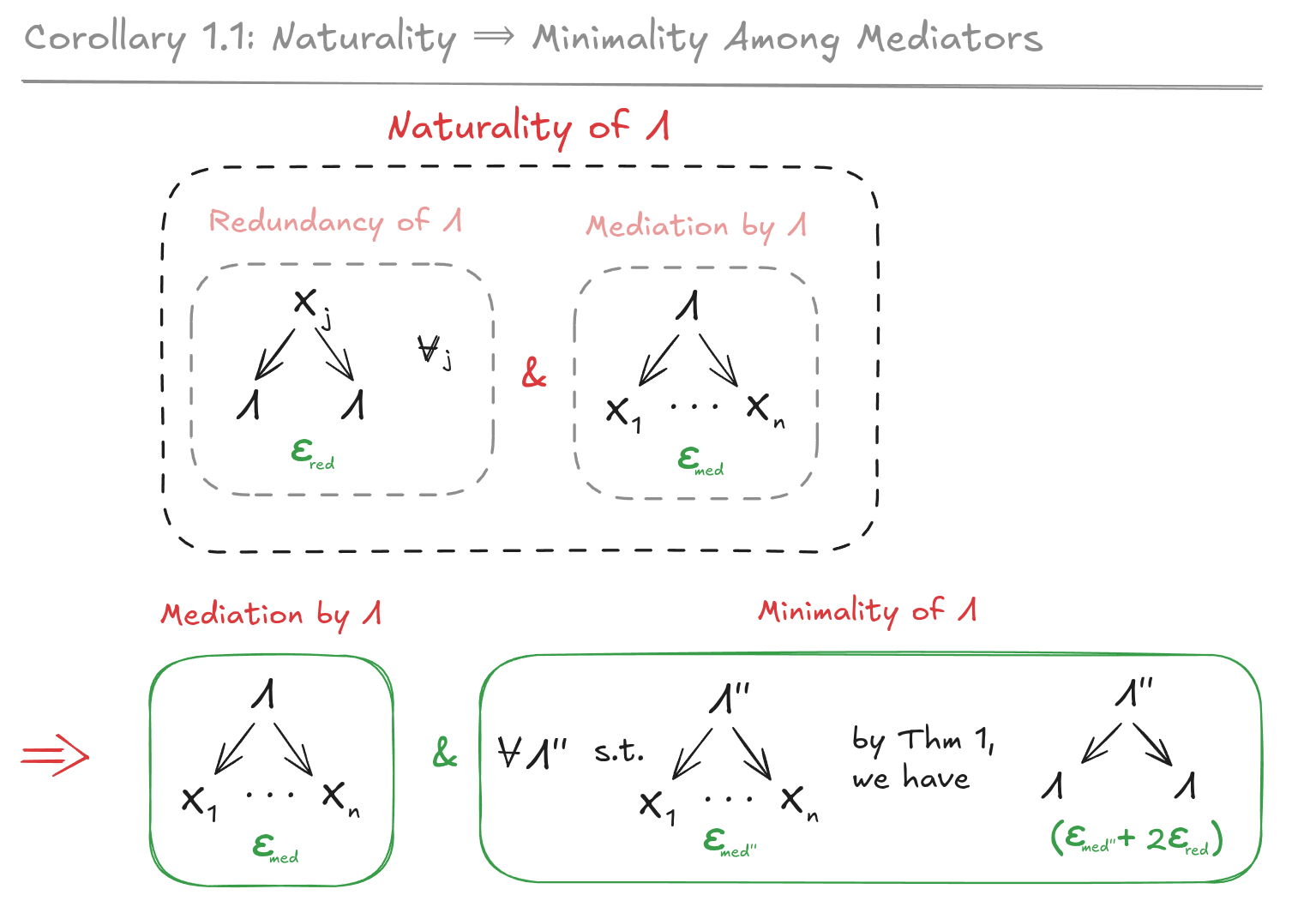
(14:51) Naturality _\\implies_ Minimality Among Mediators

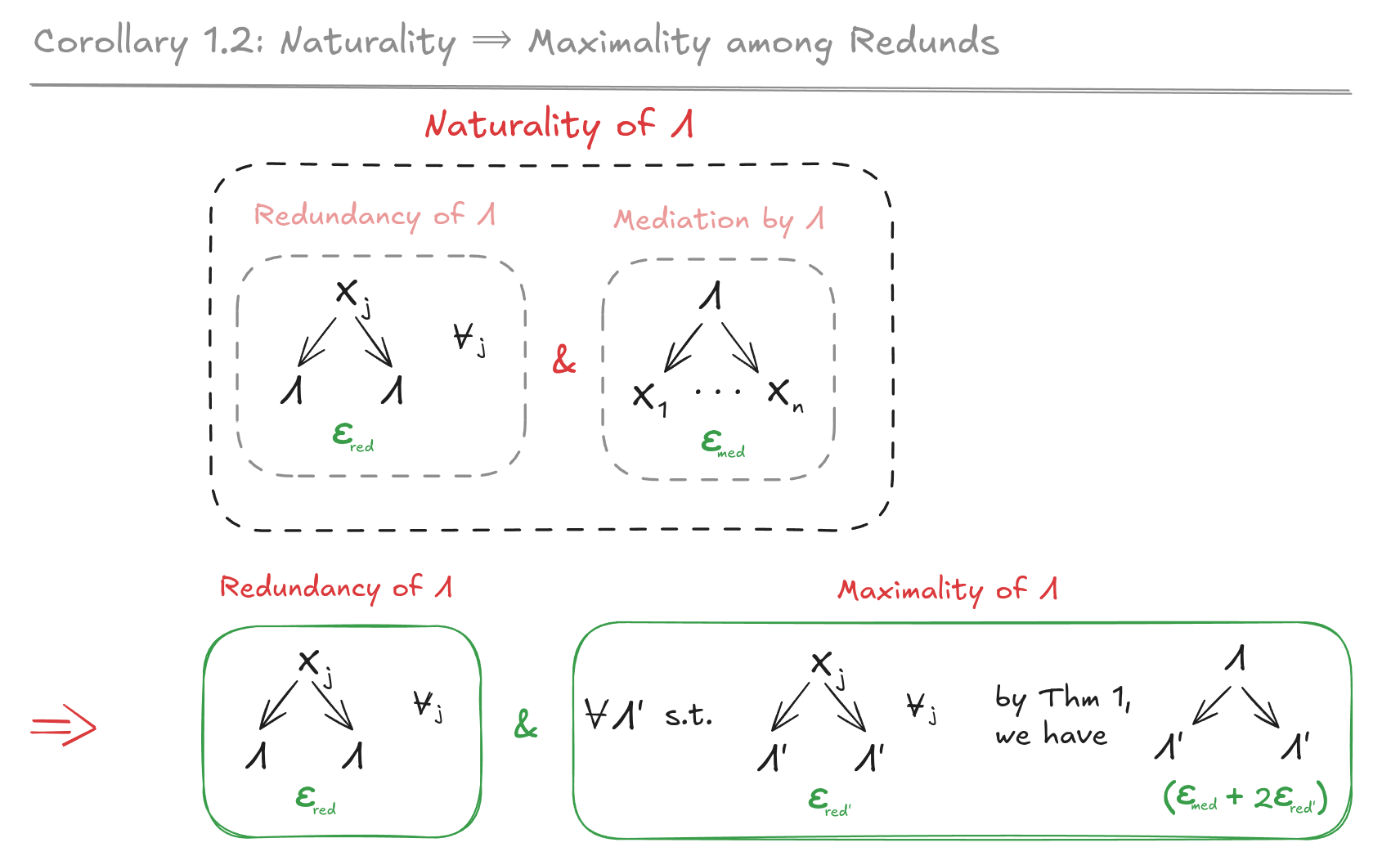
(15:59) Naturality _\\implies_ Maximality Among Redunds

(16:47) Isomorphism of Natural Latents

(17:14) Application To Translatability

(17:18) Motivating Question

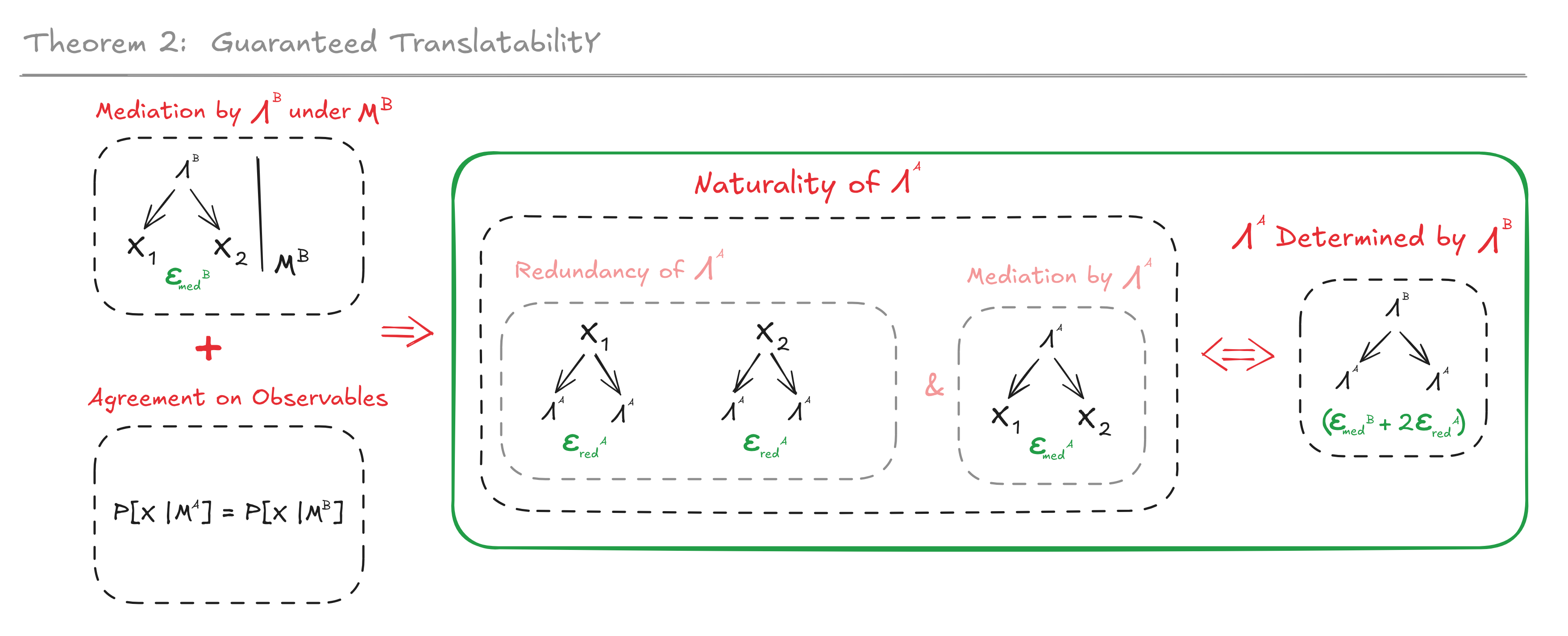
(18:27) Guaranteed Translatability

(21:09) Natural Latents: Intuition & Examples

(21:24) When Do Natural Latents Exist? Some Intuition From The Exact Case

(23:11) Worked Quantitative Example of the Mediator Determines Redund Theorem

(26:54) Intuitive Examples of Natural Latents

(27:17) Ideal Gas

(28:22) Biased Die

(29:36) Timescale Separation In A Markov Chain

(30:24) Discussion & Conclusion

(33:56) Acknowledgements

(34:05) Appendices

(34:08) Graphical Notation and Some Rules for Graphical Proofs

(35:02) Frankenstein Rule

(37:39) Factorization Transfer

(39:15) Bookkeeping Rule

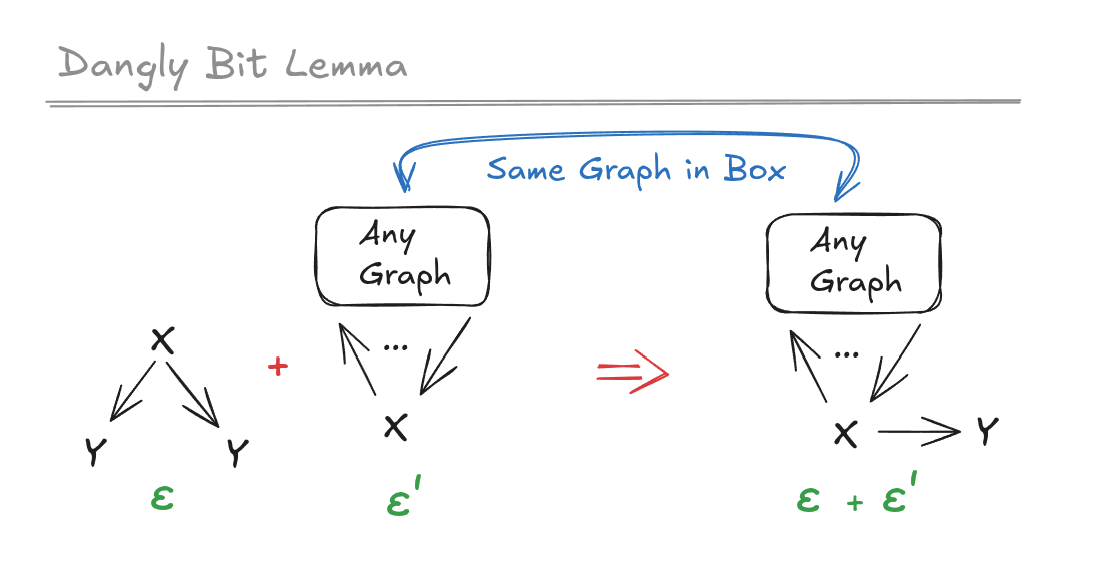
(40:03) The Dangly Bit Lemma

(41:09) Graphical Proofs

(41:18) Python Script for Computing _D_{KL}_ in Worked Example

The original text contained 5 footnotes which were omitted from this narration.

---

First published:

September 4th, 2025

Source:

https://www.lesswrong.com/posts/Qdgo2jYAuFRMeMRJT/natural-latents-latent-variables-stable-across-ontologies

---

Narrated by TYPE III AUDIO.

---

Images from the article:

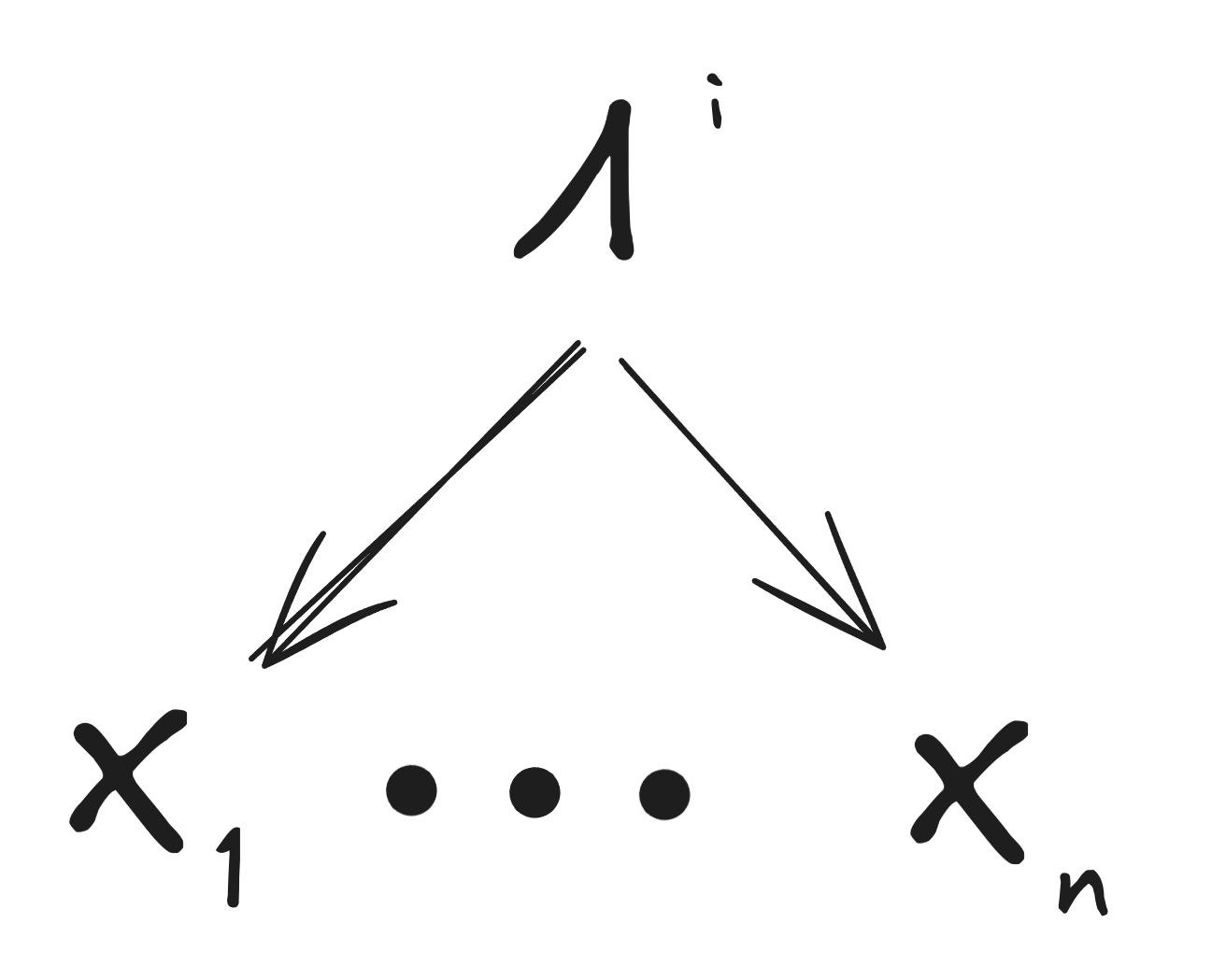__T3A_INLINE_LATEX_PLACEHOLDER___i^{th}___T3A_INLINE_LATEX_END_PLACEHOLDER__ model, graphically. A distribution __T3A_INLINE_LATEX_PLACEHOLDER___P[X_1, X_2, \Lambda^i]___T3A_INLINE_LATEX_END_PLACEHOLDER__ "satisfies" this graph if and only if it satisfies the factorization __T3A_INLINE_LATEX_PLACEHOLDER___P[X_1, X_2, \Lambda^i] = P[\Lambda^i] \prod_j P[X_j|\Lambda^i]___T3A_INLINE_LATEX_END_PLACEHOLDER__." style="max-width: 100%;" />

---

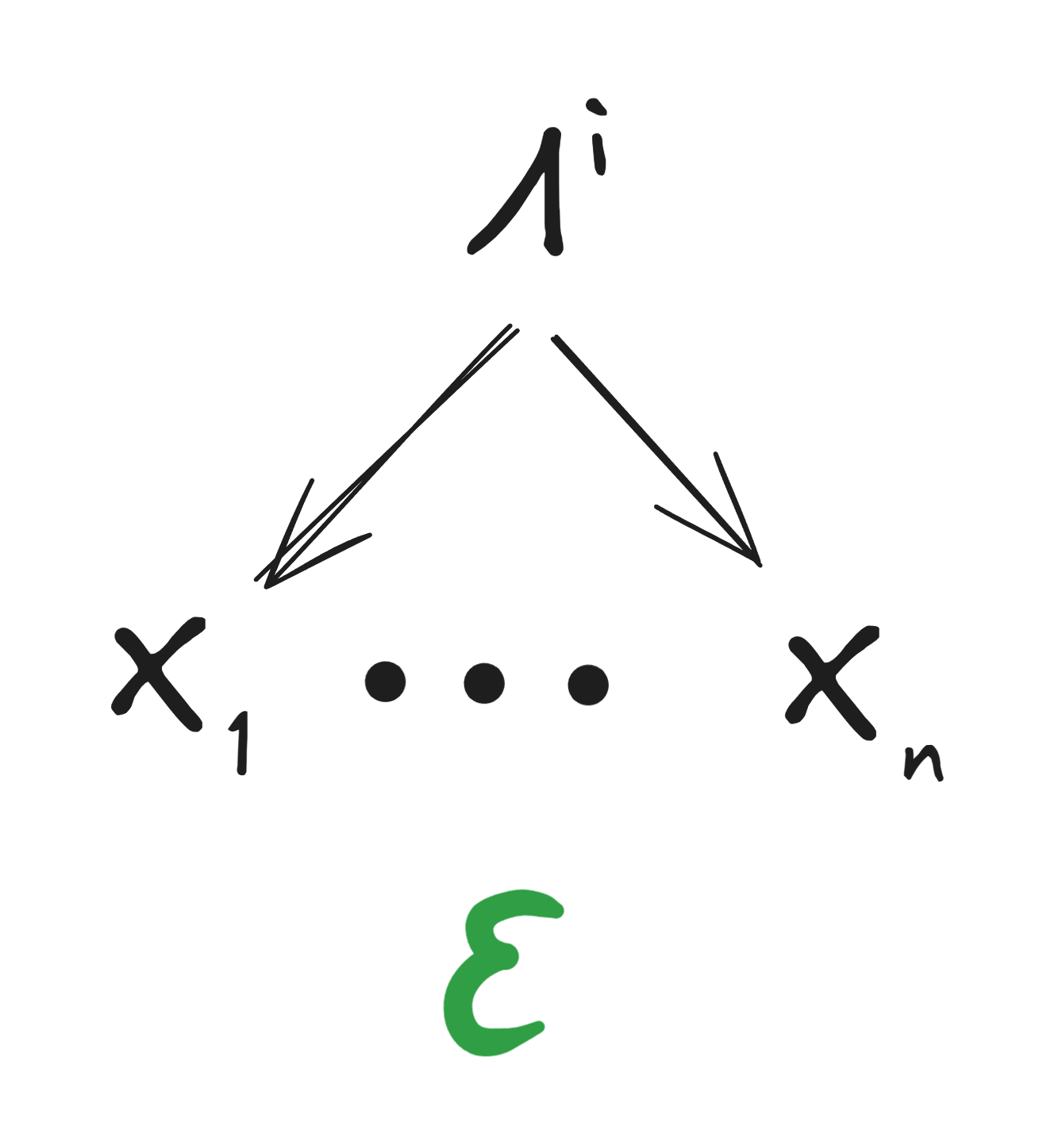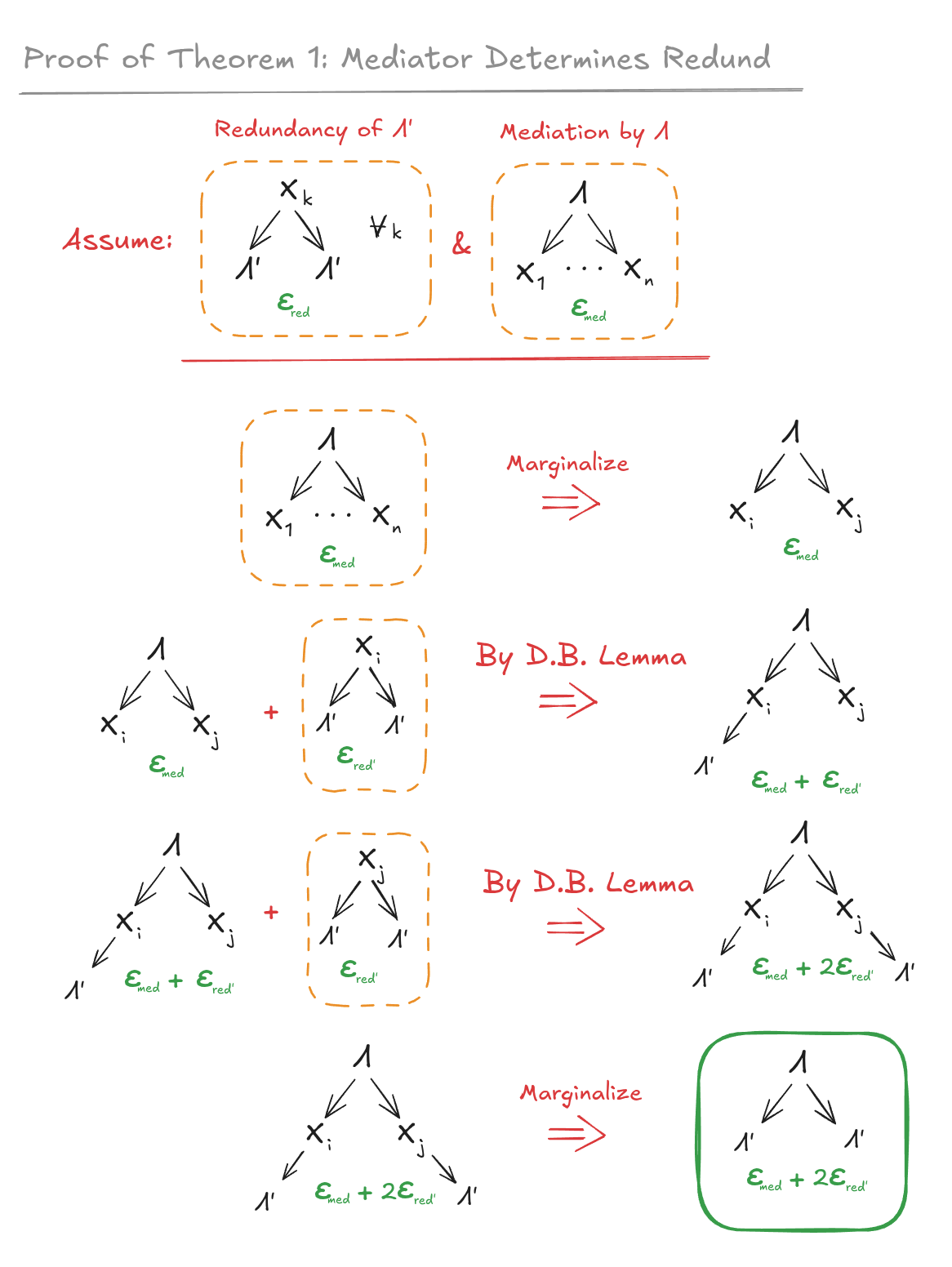
__T3A_INLINE_LATEX_PLACEHOLDER___i^{th}___T3A_INLINE_LATEX_END_PLACEHOLDER__ model, graphically with approximation __T3A_INLINE_LATEX_PLACEHOLDER___\epsilon___T3A_INLINE_LATEX_END_PLACEHOLDER__. A distribution __T3A_INLINE_LATEX_PLACEHOLDER___P[X_1, X_2, \Lambda^i]___T3A_INLINE_LATEX_END_PLACEHOLDER__ "satisfies" this graph (including the approximation) if and only if it satisfies __T3A_INLINE_LATEX_PLACEHOLDER___\epsilon \geq D_{KL}(P[\Lambda^i, X] || P[\Lambda^i]\prod_j P[X_j|\Lambda^i])___T3A_INLINE_LATEX_END_PLACEHOLDER__." style="max-width: 100%;" />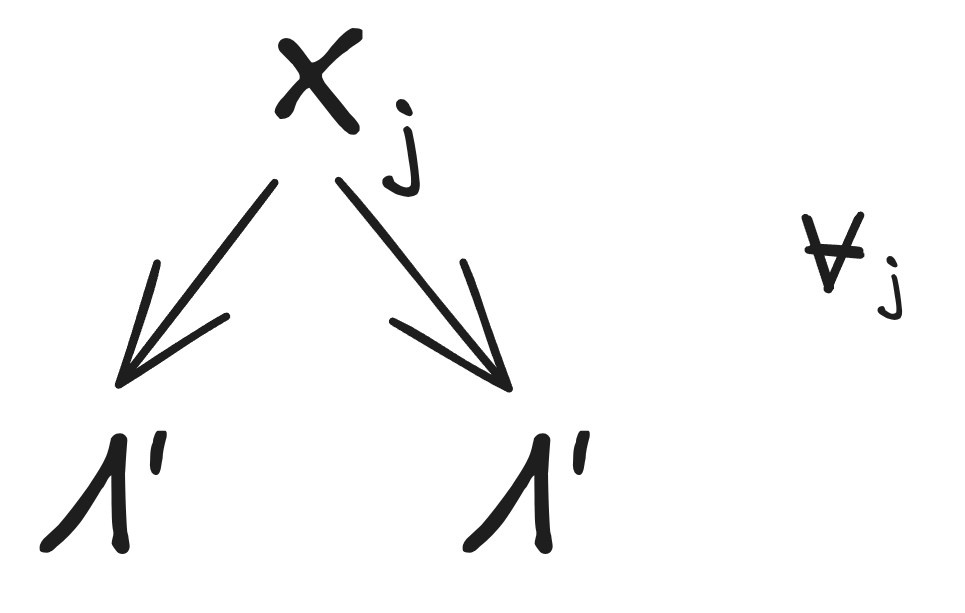

---

__T3A_INLINE_LATEX_PLACEHOLDER___\Lambda'___T3A_INLINE_LATEX_END_PLACEHOLDER__ is a "redund" over __T3A_INLINE_LATEX_PLACEHOLDER___X_1, ..., X_n___T3A_INLINE_LATEX_END_PLACEHOLDER__ if and only if __T3A_INLINE_LATEX_PLACEHOLDER___P[X, \Lambda']___T3A_INLINE_LATEX_END_PLACEHOLDER__ satisfies the graph for all __T3A_INLINE_LATEX_PLACEHOLDER___j___T3A_INLINE_LATEX_END_PLACEHOLDER__. Intuitively, it says that any one component of __T3A_INLINE_LATEX_PLACEHOLDER___X___T3A_INLINE_LATEX_END_PLACEHOLDER__ is enough to fully determine __T3A_INLINE_LATEX_PLACEHOLDER___\Lambda'___T3A_INLINE_LATEX_END_PLACEHOLDER__." style="max-width: 100%;" />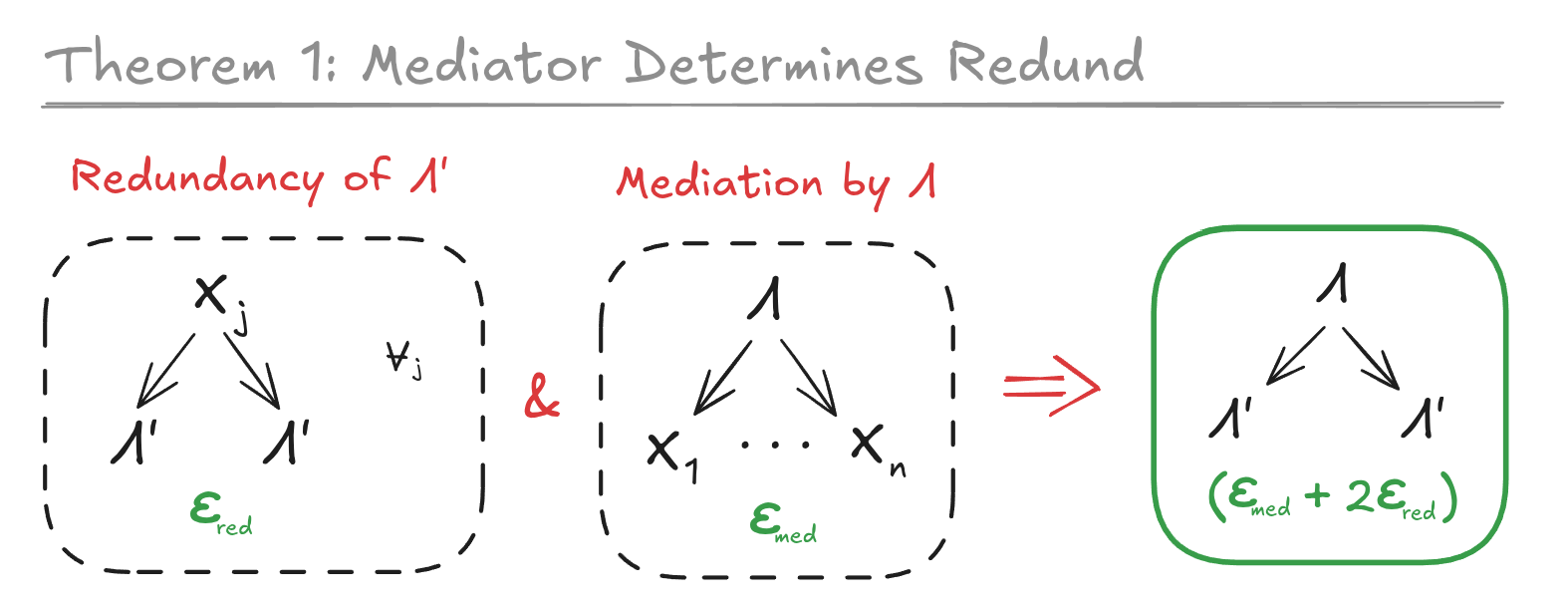

---

---

---

---

---

---

Apple Podcasts and Spotify do not show images in the episode description. Try Pocket Casts, or another podcast app.