“An Introduction to Credal Sets and Infra-Bayes Learnability” by Brittany Gelb

Audio note: this article contains 247 uses of latex notation, so the narration may be difficult to follow. There's a link to the original text in the episode description.

Introduction

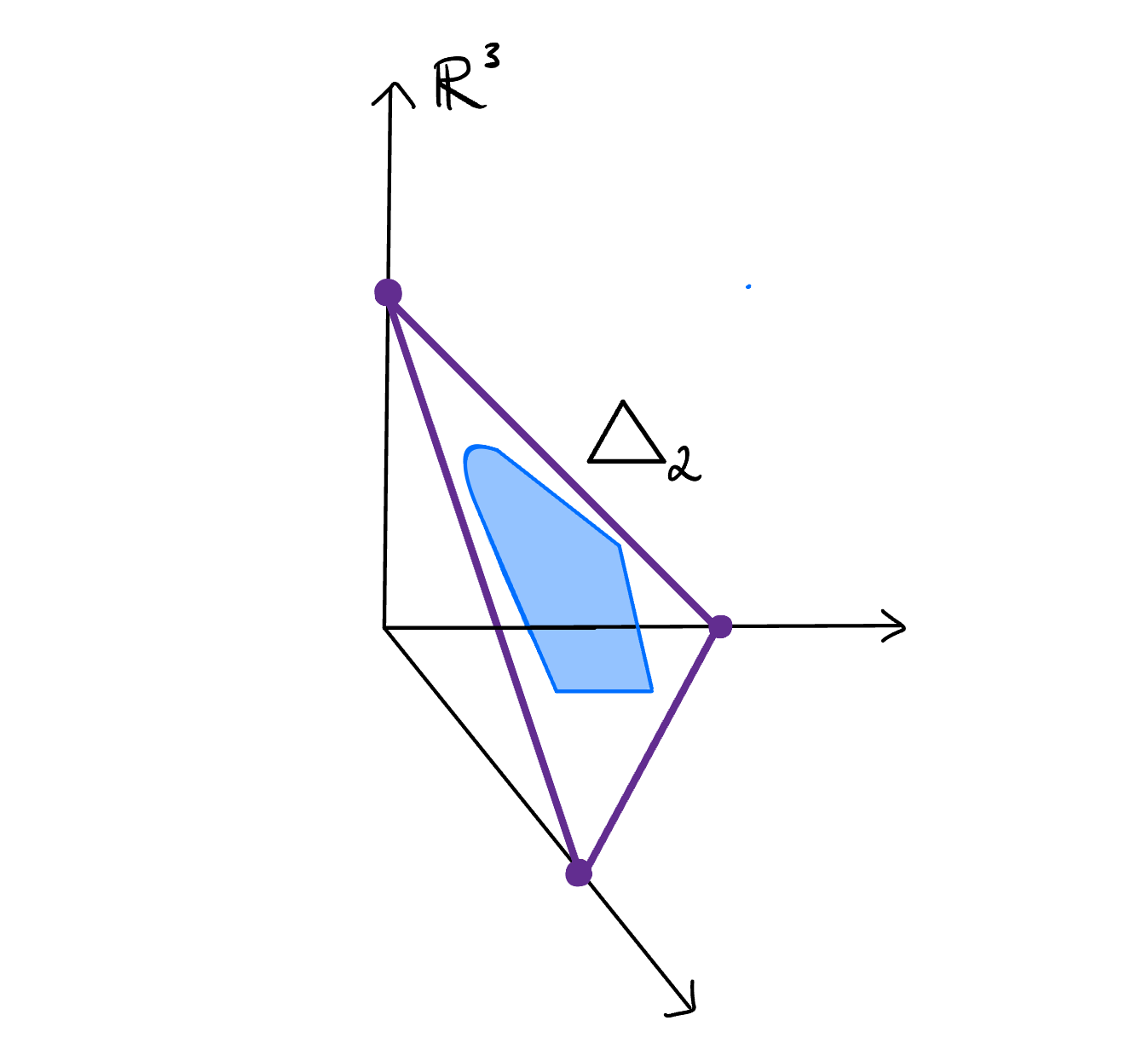
Credal sets, a special case of infradistributions[1] in infra-Bayesianism and classical objects in imprecise probability theory, provide a means of describing uncertainty without assigning exact probabilities to events as in Bayesianism. This is significant because as argued in the introduction to this sequence, Bayesianism is inadequate as a framework for AI alignment research. We will focus on credal sets rather than general infradistributions for simplicity of the exposition.

Defining Credal Sets

Recall that the total-variation metric is one example of a metric on <span>_Delta X,_</span> the set of probability distributions over a finite set <span>_X._</span> A set is closed with respect to a metric if it contains all of its limit points with respect to the metric. [...]

---

Outline:

(00:23) Introduction

(00:54) Defining Credal Sets

(07:47) Infrakernels

(09:53) Deterministic Versus Stochastic Policies

(11:51) Topologies on policies and destinies

(12:09) The topology on the set of deterministic policies

(13:07) The topology on the set of destinies

(13:49) The topology on the set of credal sets over destinies

(15:08) Crisp Causal Laws

(18:20) The Minimax Decision Rule

(20:35) Infra-Regret

(22:12) Infra-Bayes Optimality and Learnability

(25:24) Acknowledgements

The original text contained 10 footnotes which were omitted from this narration.

---

First published:

August 22nd, 2025

Source:

https://www.lesswrong.com/posts/rkhaRnAc6dLzQT2sJ/an-introduction-to-credal-sets-and-infra-bayes-learnability-1

---

Narrated by TYPE III AUDIO.

---

Images from the article:

---

---

---

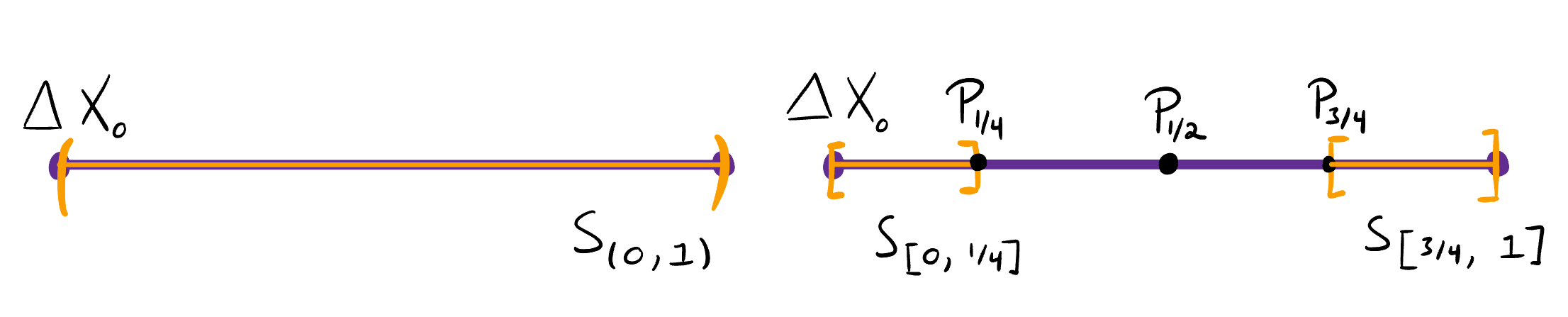
Apple Podcasts and Spotify do not show images in the episode description. Try Pocket Casts, or another podcast app.